পাই। বৃত্তের পরিধি ও ব্যাসের অনুপাত। সংখ্যাটি ধ্রুব, কিন্তু অমূলদ। অর্থাৎ, পাই এর মান ভগ্নাংশ আকারে প্রকাশ করা যায় না।

মাধ্যমিক পর্যায়ে যখন পাই(π) সম্পর্কে প্রথম জানতে পারি তখন থকেই সংখ্যাটি নিয়ে একপ্রকার কৌতুহল কাজ করতো। চেষ্টা করতাম এমন কোনো সূত্র বের করা যায় কিনা যার দ্বারা পাইয়ের অ্যাকুরেট মান বের করা সম্ভব। বাস্তবে যদিও সেটা সম্ভব নয়। তারপরও সাইন্টিস্টরা কিছু ইনফিনিট সিরিজ বের করেছেন যেগুলোর দ্বারা পাইয়ের অ্যাপ্রোক্সিমেট মান বের করা সম্ভব। যেমন: গ্রেগরি-লিবনিজ সিরিজ বা Bailey-Borwein-Plouffe (BBP) formula.

কিন্তু রিয়াল লাইফেতো আর আমাদের পক্ষে কোনো সিরিজের ইনফিনিট সংখ্যক টার্ম যোগ করা সম্ভব নয়। তাছাড়া ফর্মূলাগুলো বেশ জটিল ও মুখস্ত রাখাটা কষ্টসাধ্য।

পাইয়ের অ্যাপ্রোক্সিমেট (কিন্তু নিয়ারলি অ্যাকুরেট) মান বের করার জন্য একটি সহজ ফর্মূলা বের করা যায় কিনা সেই চেষ্টাই করছিলাম। পাই নিয়ে চিন্তা করতে করতে এর মান বের করার জন্য ভালো একটি আইডিয়া হঠাৎ একদিন চলেও এলো মাথায়। সেই আইডিয়াটিই সবার সাথে শেয়ার করতে চাচ্ছি।

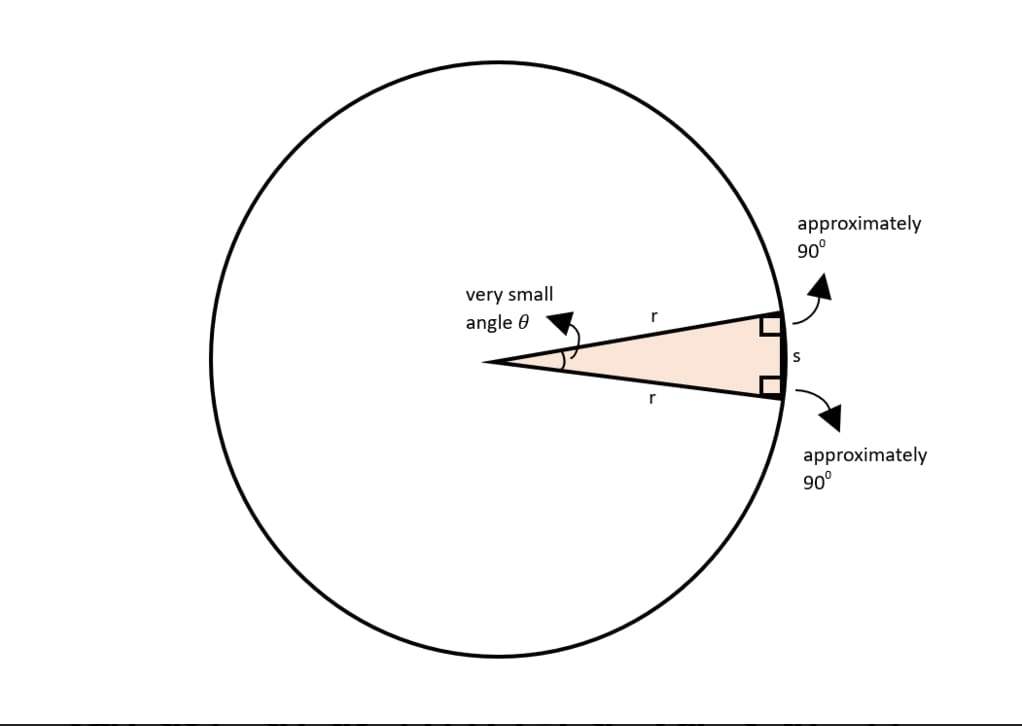
একটি বৃত্তের কেন্দ্র হতে পরিধি পর্যন্ত একটি ত্রিভুজ আঁকা যাক (চিত্রের অনুরূপ) যার কেন্দ্রস্থ কোণ θ খুবই খুদ্র ( θ0 )। ত্রিভুজটি একটি সমদ্বিবাহু ত্রিভুজ। আমরা জানি ত্রিভুজের তিন কোণের সমষ্টি 1800। তাহলে ত্রিভুজের পরিধি সংলগ্ন উভয় কোণের মান ≈900 । আমরা ত্রিভুজটিকে একটি সমকোণী ত্রিভুজ বিবেচনা করতে পারি যার দুটি কোণের মান 900 এবং ত্রিভুজের অতিভুজ ও ভূমি উভয়ের দৈর্ঘ্য হলো বৃত্তের ব্যাসার্ধ (r)। এবং কেন্দ্রস্থ কোণ θ দ্বারা উৎপন্ন বৃত্তচাপ s, যেটি ত্রিভুজের তৃতীয় বাহু (s0)।

ত্রিভুজটির উপর ত্রিকোণমিতিক সূত্র অ্যাপ্লাই করে পাই, sin θ ≈ লম্ব/অতিভূজ ≈ s/r

 s ≈ r.sinθ ………(i)

এখন, s বৃত্তচাপ দ্বারা কেন্দ্রে উৎপন্ন কোণ θ০। পরিধি দ্বারা কেন্দ্রে উৎপন্ন কোণ 360০।

যেহেতু বৃত্তচাপের দৈর্ঘ্য সর্বদা উক্ত বৃত্তচাপ দ্বারা কেন্দ্রে উৎপন্ন কোণের সমানুপাতিক,অতএব, পরিধি/s = 360০/θ০

পরিধি = 360*s/θ = (360*r.sinθ)/θ …(ii)

(placing value of s from (i) no eqn)

পরিধি/ব্যাস = (360*r.sinθ)/(θ*ব্যাস)

pi = (360*r.sinθ)/(θ* 2r)

 π = (360*sinθ)/(2θ) ………(formula!)

যেখানে, θ tends to 0

ক্যালকুলেটরে উক্ত ফর্মুলাটি বসিয়ে দেখতে পারো, যেখানে θ এর ভ্যালু খুবই খুদ্রে। pi এর অ্যাপ্রোক্সিমেট ভ্যালু পেয়ে যাবে। এবং, এই ক্ষেত্রে θ এর ভ্যালু যত ছোট বসাবে অ্যাকুরেসি ততোই বেশি হবে।

উদাহরণস্বরূপ, θ এর ভ্যালু 10^(-1) এর জন্য pi এর মান পাওয়া যায় 3.1415910… (দশমিকের পর 5 ঘর পর্যন্ত অ্যাকুরেট।)

আবার, θ এর ভ্যালু 10^(-3) এর জন্য pi এর মান পাওয়া যায় 3.14159265343… (দশমিকের পর 9 ঘর পর্যন্ত অ্যাকুরেট।) (হিসাব অবশ্যই ডিগ্রি মোডে রেখে করতে হবে)

এভাবে θ কোণের ক্ষুদ্র ক্ষুদ্র ভ্যালু ক্যালকুলেটর বা কম্পিউটার সফটওয়্যারে বসিয়ে দেখতে পারো কতদূর পর্যন্ত pi এর অ্যাকুরেট মান পাওয়া যায়!